Kapitel 10 Inferenzstatistik
10.1 Anknüpfungspunkte
- Signifikanztest
- Lagemaße
- Streuungsmaße
- z-Transformation
10.2 Vorbereitung
10.3 Allgemeines
- Ziel: Schluss von den erhobenen Daten einer Stichprobe auf die Werte in der Population
10.3.1 Schätzer
- Punktschätzung: Angabe eines Werts für einen unbekannten Parameter
- Erwartungswert \(E(X)\)
- Probleme: (fast) sicher falsch, keine Aussage über Genauigkeit
- Intervallschätzung: Angabe eines Intervalls, das mit einer bestimmten Wahrscheinlichkeit den unbekannten Parameter überdeckt.
- Konfidenzintervall (confidence interval, CI): Der Wertebereich, in dem man den interessierenden Parameter der Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit erwartet, bezeichnet man als Konfidenzintervall.
- Hypothesentest: Annahme bzw. Zurückweisung von Aussagen über den unbekannten Parameter bei einer vorgegeben Irrtumswahrscheinlichkeit
10.4 Standardfehler (SE) des Mittelwerts
- Genauigkeit der Schätzung: Der Standardfehler des Mittelwerts gibt die Genauigkeit der Schätzung des Populationsmittelwerts an. Aufgrund einer Stichprobe können wir nicht nur den Mittelwert der Population schätzen, sondern auch die Genauigkeit dieser Schätzung bestimmen.
- Streuung in einer Verteilung: Der Standardfehler ist definiert als die Streuung in einer Verteilung von Mittelwerten aus gleich großen Zufallsstichproben einer Population.
- Je kleiner der Standardfehler, desto präziser die Schätzung des Populationsparameters
- Standardfehler wird größer…
- je größer die Streuung der Messwerte \(\sigma\)
- je kleiner die Stichprobe \(n\)
\[ SE = \frac{\sigma}{\sqrt{n}} \approx \frac{s}{\sqrt{n}}\]
10.5 Konfidenzintervall (CI)
- Der Konfidenzintervall ergibt sich aus
- der gesetzten Breite des Intervalls \(z\) (\(\alpha\)-Level) - Per Konvention: z = 1,96 (95%) oder 2,58 (99%), siehe z-Transformation
- dem Stichprobenmittelwert \(\bar{x}\)
- dem geschätzen Standardfehler \(SE_{\bar{x}}\) \[ lower limit (LL) = \bar{x} - z * SE_{\bar{x}} \] \[ upper limit (UL) = \bar{x} + z * SE_{\bar{x}} \]
- Interpretation: Misst man mehrmals und berechnet jeweils den 95% CI, enthalten 95% der Intervalle den Populations-Mittelwert.
- falsche Interpretation: “Mit einer Wahrscheinlichkeit von 95% liegt der Populations-Mittelwert innerhalb von dem CI”
10.6 Konfidenzintervall (CI) - Berechnungsbeispiel in R
data <- c(1, 2, 10, 5, 20, 3)
m <- mean(data)
sd <- sd(data)
n <- length(data)
SE <- sd/sqrt(n)
(LL <- m - 1.96*SE)## [1] 1.1## [1] 13Der 95% Konfidenzintervall um den Mittelwert 6.83 reicht von 1.08 bis 12.59.
10.7 Konfidenzintervall (CI) - Weite
- Die Länge des Konfidenzintervalls (UL-LL) hängt ab von
- \(\alpha\)-Level / z: Je größer das Alpha-Level, desto weiter das CI
- \(\sigma\): Je größer die Standardabweichung, desto weiter das CI
- n: Je größer die Stichprobe, desto kürzer das CI
\[ UL - LL = \bar{x} + \alpha*SE -(\bar{x} - \alpha*SE) = 2*\alpha*SE = \frac{2*\alpha*\sigma}{\sqrt{n}} \]
- Interpretation: ein weites CI ist “ungenauer”!
10.8 Demonstration von Population, Stichprobenziehung, Standardfehler
10.8.1 Population
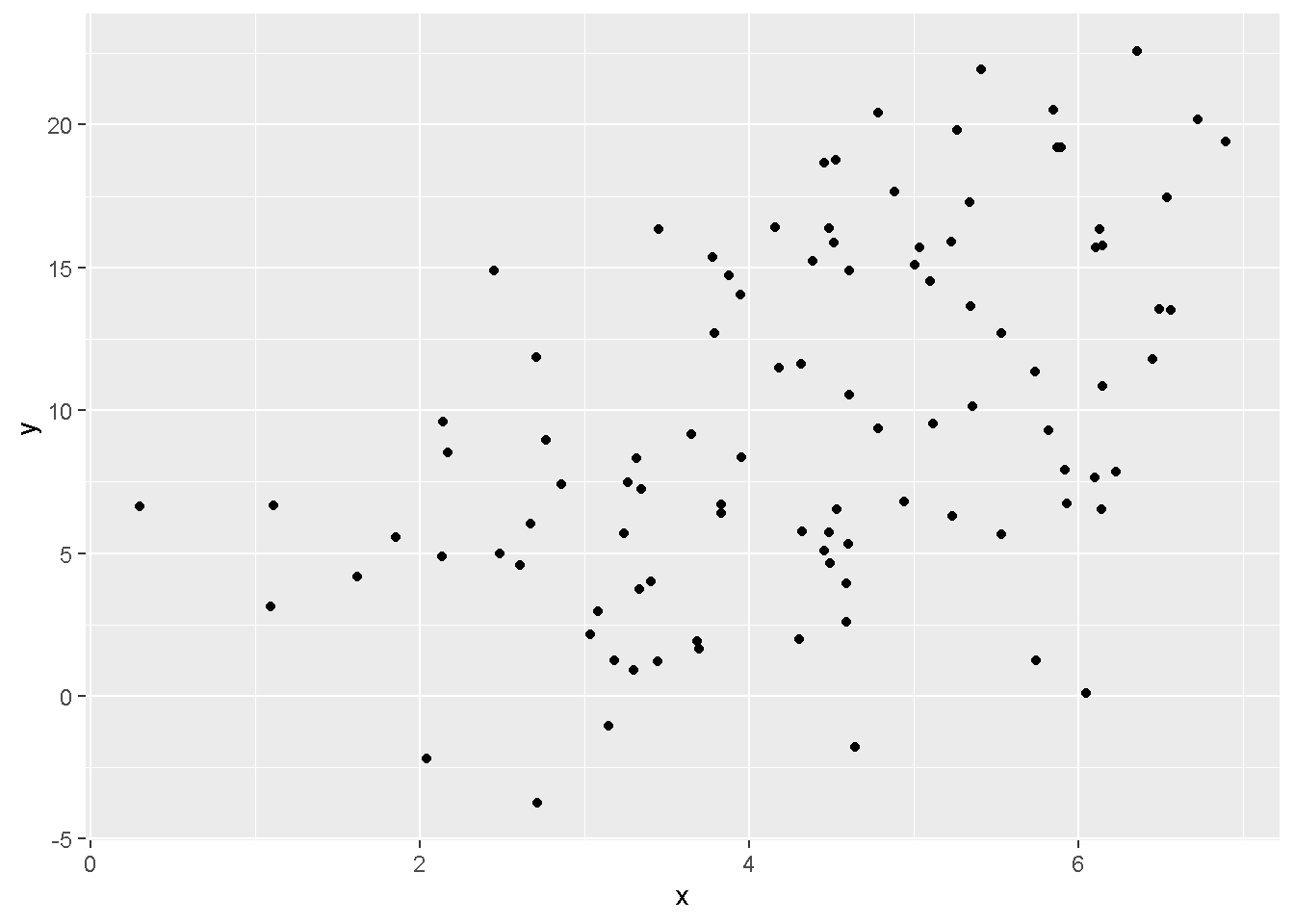
## Warning: package 'truncnorm' was built under R version 4.0.3Wir generieren eine Punktwolke, die für diese Demonstration unsere Grundgesamtheit darstellt. Es sind 100 Datenpunkte mit 2 Variablen x und y. Die Regressionsgleichung der Population ist:
\[ y = 1 + 2x + e \]
Hier ist die Punktewolke dargestellt:
10.8.2 Stichprobe
Wir ziehen nun 4 Stichproben (ca. 0.1 der Population werden jeweils gesampelt) von dieser Grundgesamtheit (rote Punkte) und zeichnen die Regressionsgerade ein (rote Linie). Die Stichproben sind immer anders, und daraus ergibt sich auch ein andere Regressionslinie. Der Konfidenzintervall (grauer Bereich) verändert sich ebenfalls um die Regressionslinie herum – je nachdem wie, die Stichprobe gestreut ist.
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'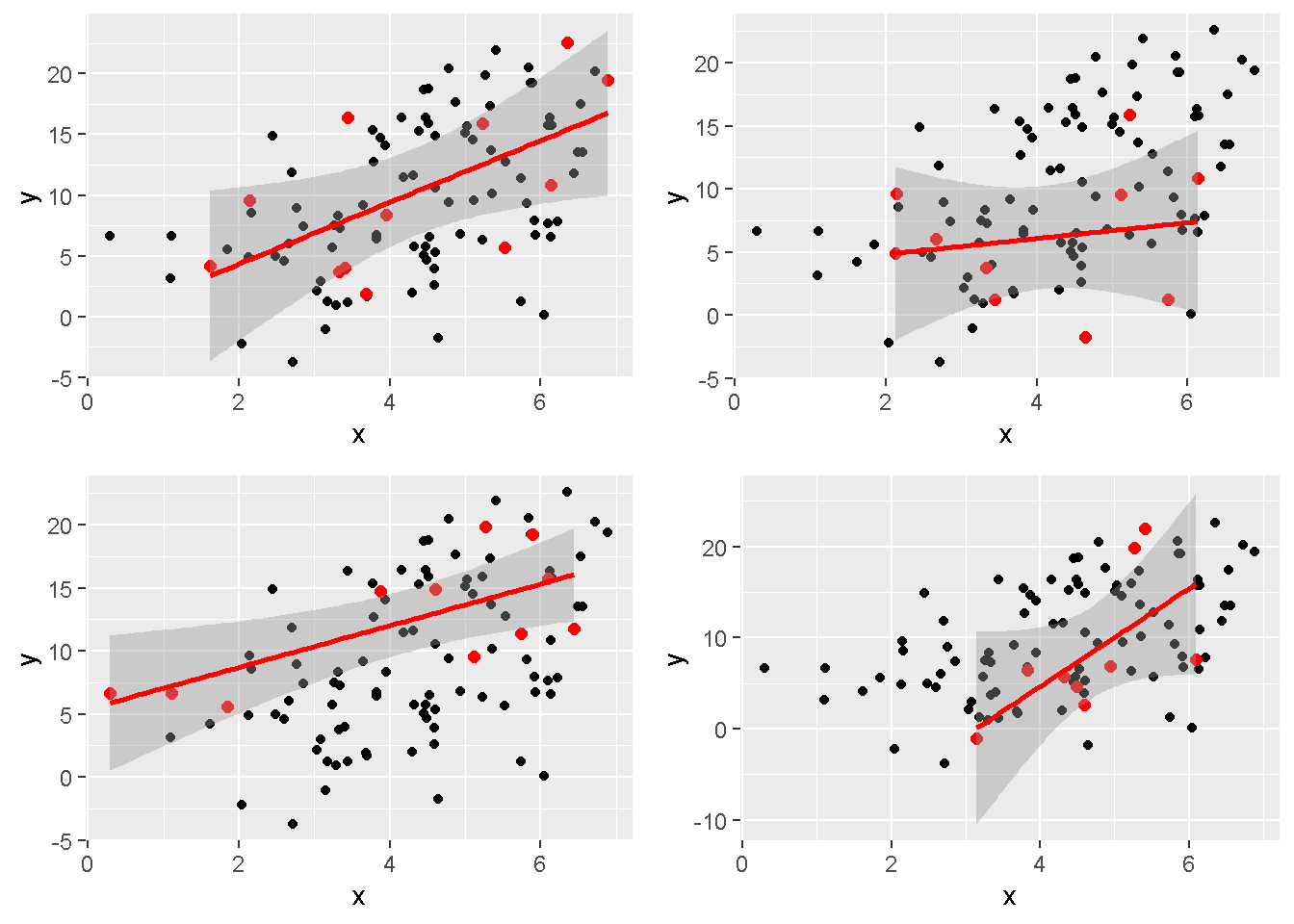
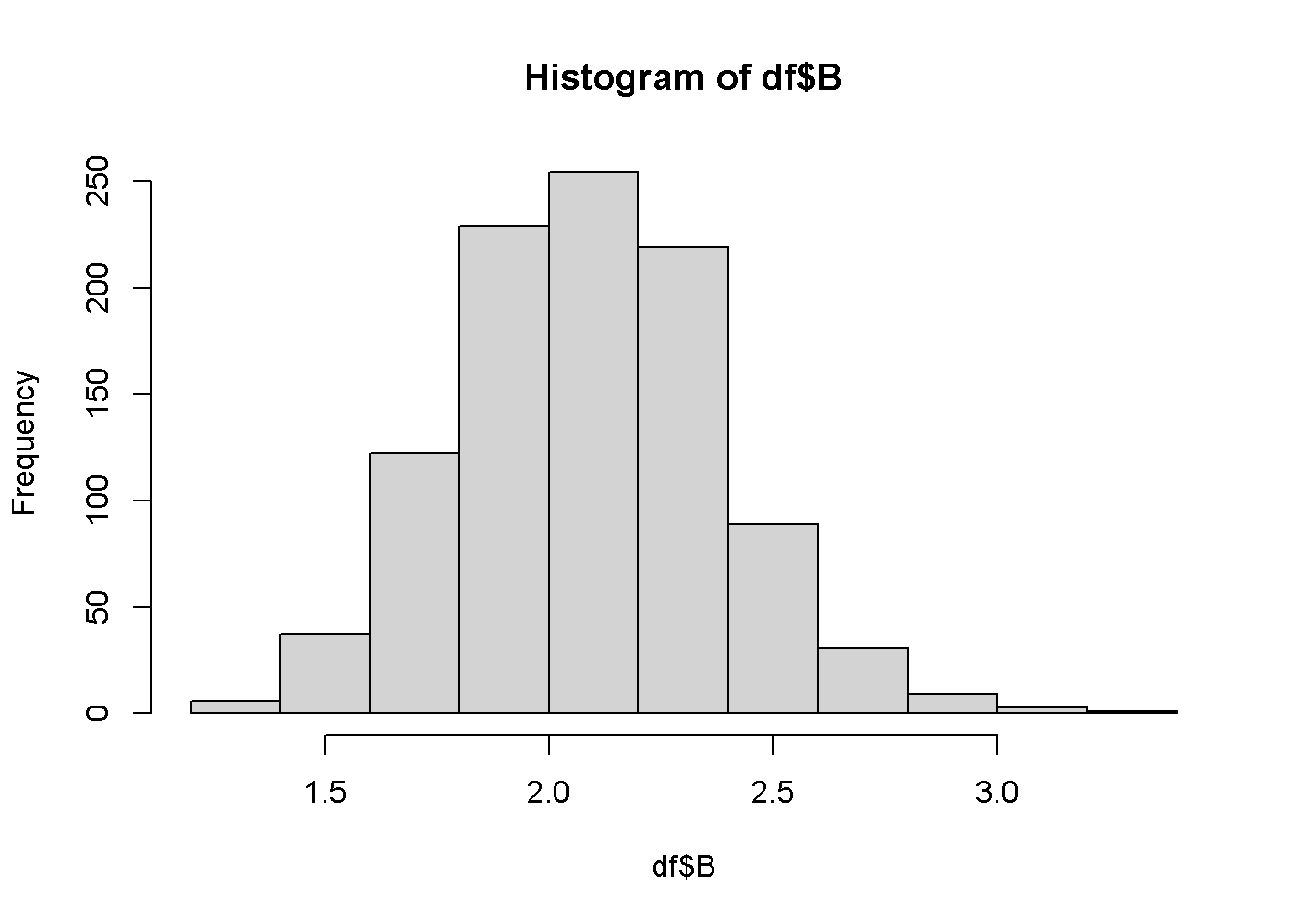
Im Histogramm werden die B-Werte aller Stichproben gesammelt.

10.8.3 Größere Stichprobe
Jetzt wiederholen wir den Versuch mit eine größeren Stichprobe (ca. 0.6 der Population werden jeweils gesampelt).
Frage: Wie verändern sich die Standardfehler?
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
10.9 Übung
- Lade die Daten Froehlich et al. 2014 Daten 100.sav
- Berechne eine neue Variable: MWC = der Mittelwert von WC1-WC7. Welchen Wert hat Fall 3?
- Welches Messniveau hat MWC?
- Berechne den Standardfehler mit der Hand und kontrolliere den Wert in SPSS.
- Erstelle ein Diagramm, das MWC in Balken (inkl. 99% Konfidenzintervall) für die einzelnen Banken (DBAN) zeigt. Welche Bank hat den höchsten MWC Wert (ohne Fehler)?
10.10 Lösung
- Transformieren, Variable Berechnen, MEAN(WC1, WC2,.). 3,85714285714286
- Metrisch.
- SPSS: via Häufigkeiten, Mit der Hand: Standardabweichung / Wurzel(n). SE = ,05948
- Bank 3