Kapitel 9 Verteilungen
9.1 Anknüpfungspunkte
- Lagemaße
- Streuungsmaße
9.2 Vorbereitung
9.3 Normalverteilung
- wichtige Voraussetzung: Die Annahme der Normalverteilung ist Voraussetzung für viel der weiteren Überlegungen der Inferenz- und Teststatistik
- Sehr viele Merkmale sind normalverteilt: Körpergröße, Intelligenz, Sehvermögen etc.
- Kennzeichen
- unimodal/eingipfelig
- glockenförmiger Verlauf
- symmetrisch: Median, Modus und arithmetisches Mittel sind identisch
9.4 Zentraler Grenzwertsatz
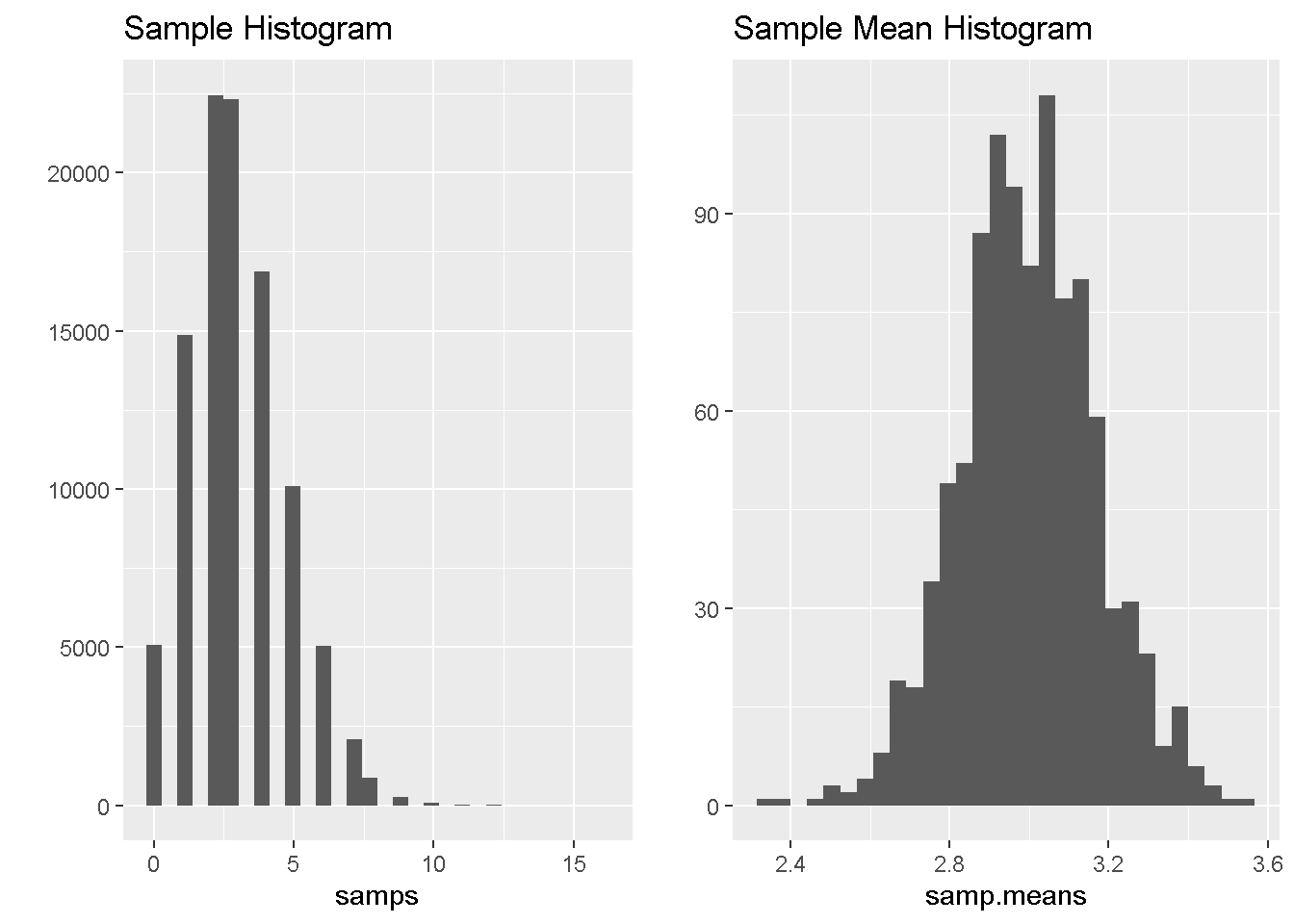
- Die Verteilung von arithmetischen Mittelwerten aus Stichproben derselben Grundgesamtheit vom Umfang n geht mit wachsendem n in eine Normalverteilung über.
- Die Annäherung an die Normalverteilung gilt ab n>30 (Daumenregel)
- Video-Demonstration
9.5 Zentraler Grenzwertsatz - Demonstration, uniforme Verteilung

9.6 Zentraler Grenzwertsatz - Demonstration, Poisson Verteilung
9.7 Standardnormalverteilung
- X ~ N (0;1)
- Erwartungswert E(X) = 0
- Varianz (Var) = Standardabweichung (SD) = 1
9.7.1 Wichtige Punkte der Normalverteilung
- [-1SD, 1SD] = 68%
- [-1,96SD, 1,96SD] = 95%
- [-2,58SD, 2,58SD] = 99%
9.8 Standardnormalverteilung - Visualisierung

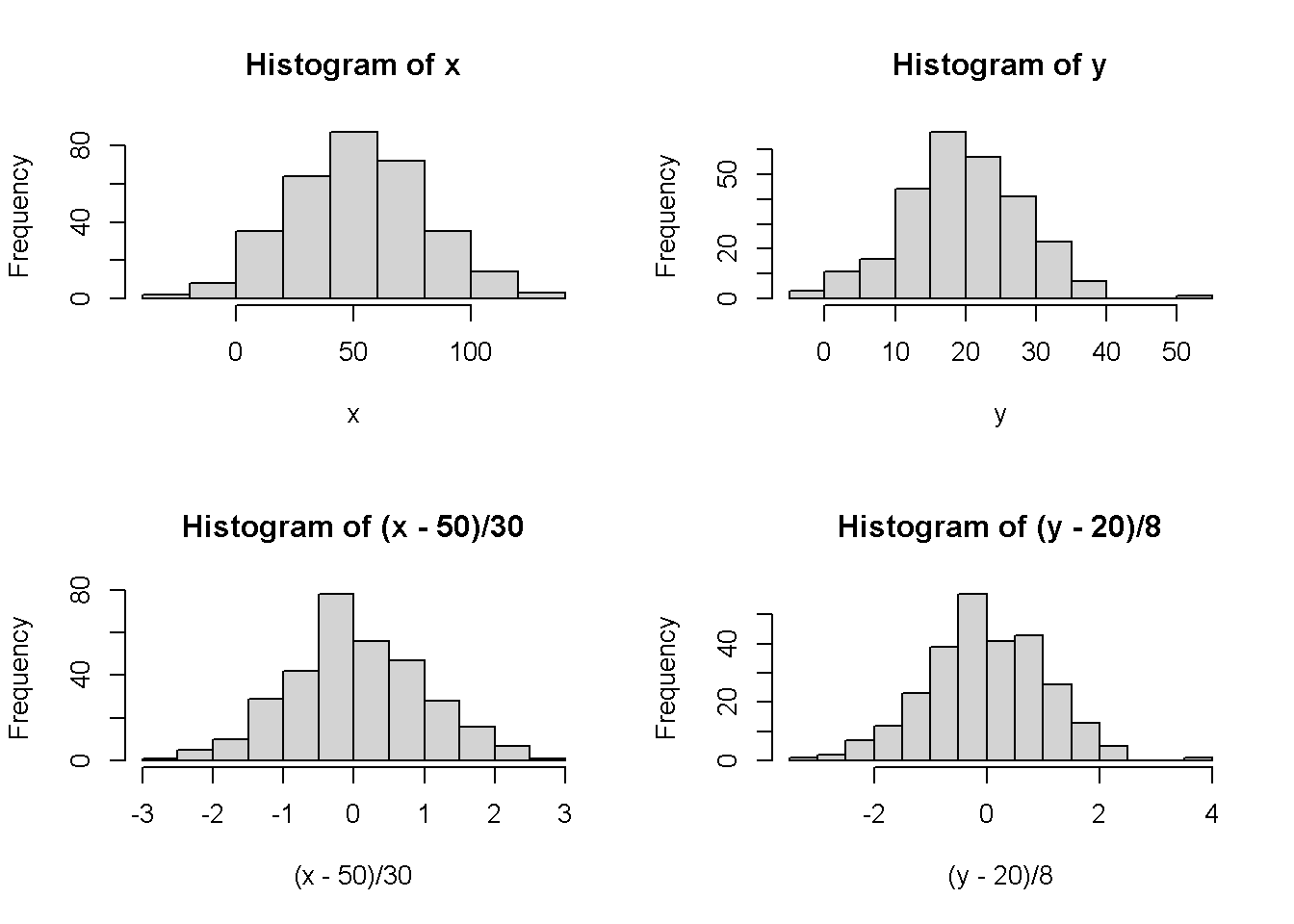
9.9 z-Transformation
- Überführung einer Normalverteilung in die Standardnormalverteilung
\[ z = \frac{X - \bar{X}}{SD} \]
Interpretation der Formel: Zentrieren der Daten um 0; Dividieren durch die Standardabweichung um sicherzustellen, dass die Standardabweichung 1 ergibt.
9.10 z-Transformation - Beispiel
9.11 Wieso Standardisierung?
- Vergleichbarkeit: Auf der Basis der z-Werte ist es problemlos möglich, die Ergebnisse mehrerer auf unterschiedlichen Normalverteilungen basierender Messinstrumente zu vergleichen.
- Wahrscheinlichkeiten ablesbar: Anhand der Standardnormalverteilungstabelle lassen sich die zu den z-Werten dazugehörigen Wahrscheinlichkeiten ablesen. Jedem z-Wert ist dort eine Fläche unter der Kurve zugeordnet, die dieser z-Wert nach links abschneidet - diese Fläche ist identisch mit der Wahrscheinlichkeit dafür, aus einer Population zufällig einen Wert zu ziehen, der kleiner oder gleich diesem z-Wert ist. Um die Wahrscheinlichkeit eines Intervalls zu bestimmen, muss man die Wahrscheinlichkeiten der z-Werte, die die Grenzen des Intervalls festlegen, voneinander subtrahieren.
9.12 Übung mit Software
- Öffne den Datensatz “Froehlich et al 2014 Daten 100.sav” mit einem Statistik-Programm deiner Wahl.
- Stelle die Variable LASD1 im Histogramm dar.
- Ist die Kurve (ungefähr) normalverteilt?
- Berechne eine neue Variable SD, die den Mittelwert von LASD1-LASDn bildet.
- Stelle die Variable SD im Histogramm dar.
- Ist die Kurve (ungefähr) normalverteilt?
- Basierend auf dieser Übung, wie interepretierst du die Sinnhaftigkeit von Skalen (gegenüber einzelnen items)?
9.13 Lösung der Übung
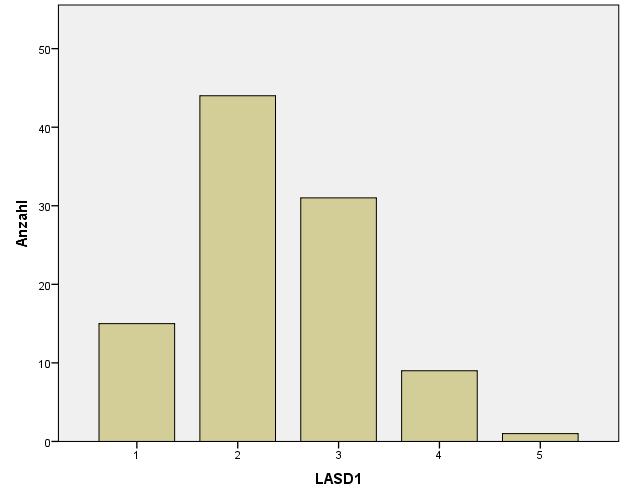
Histogramm LASD1 in SPSS
9.13.1 Bildung des Mittelwerts (SPSS Syntax)
COMPUTE SD=MEAN(LASD1, LASD2, LASD3, LASD4, LASD5, LASD6, LASD7, LASD8, LASD9, LASD10). EXECUTE.
Alternativer Syntax:
- Daten sortieren
- MEAN(LASD1 to LASD10)
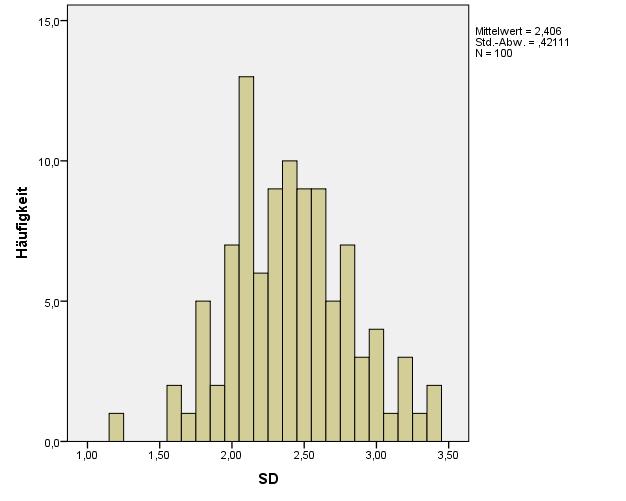
Histogramm SD in SPSS