Kapitel 19 Logistische Regression
Die binäre logistische Regression ist vom Modell her ähnlich wie eine lineare Regression. Der wichtigste Unterschied ist, dass unsere abhängige Variable dichotom (binär) ist.
19.1 Odds und Log(Odds)
- Wahrscheinlichkeit (p) ist die Gegenüberstellung eines möglichen Resultates X gegenüber allen möglichen Resultaten.
- p = X/(X + nX)
- Odds stellen die Ratio von Resultat X und nicht Resultat X (nX) dar
- odds = X/nX
- Odds haben aber ein Problem der Asymmetrie: e.g. 1/6 und 6/1 betrachten das selbe Phänomen aus der anderern Perspektive, scheinen aber ganz unterschiedliche Zahlen zu sein. Log(Odds) behebt dieses Problem: log(1/6) = -1.79, log(6/1) = +1.79. Beide Zahlen sind gleich weit weg von 0 (=Symmetrie!).
19.2 Beispiel
19.2.1 Daten
Für das Beispiel laden wir die Daten “regression1.csv” und dichotomisieren die Variable y (und setzen sie auch gleichzeitig als Faktor).
##
## 0 1
## 100 10019.2.2 Einfache binäre logistische Regression: y.bi ~ sex
##
## Call:
## glm(formula = y.bi ~ sex, family = "binomial", data = df)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.2013 -1.2013 0.0018 1.1537 1.2049
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.0645 0.2075 -0.31 0.76
## sex1 0.1206 0.2837 0.43 0.67
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 277.26 on 199 degrees of freedom
## Residual deviance: 277.08 on 198 degrees of freedom
## AIC: 281.1
##
## Number of Fisher Scoring iterations: 3- deviance gibt Auskunft über den “Fit”
19.2.3 Binäre logistische Regression: y.bi ~ x1 + x2 + sex
##
## Call:
## glm(formula = y.bi ~ x1 + x2 + sex, family = "binomial", data = df)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4824 -1.1555 0.0246 1.1586 1.4651
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.0713 0.2097 -0.34 0.73
## x1 0.2377 0.1474 1.61 0.11
## x2 0.1628 0.1490 1.09 0.27
## sex1 0.1234 0.2866 0.43 0.67
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 277.26 on 199 degrees of freedom
## Residual deviance: 273.23 on 196 degrees of freedom
## AIC: 281.2
##
## Number of Fisher Scoring iterations: 4Interpretation log odds: - Logra - Wahrscheinlichkeit p = 80% -> Odds Ratio p/(1-p) = 80%/20% = 4 -> Log Odds Ln(4) = 1.39 (50% = 0)
- AIC: Vergleiche verschiedener Modelle
- Fisher Scoring: Wie schnell war die Lösung da?
Effect Size: McFadden’s Pseudo R2
## [1] 0.015## [1] 119.2.4 Visualisierung
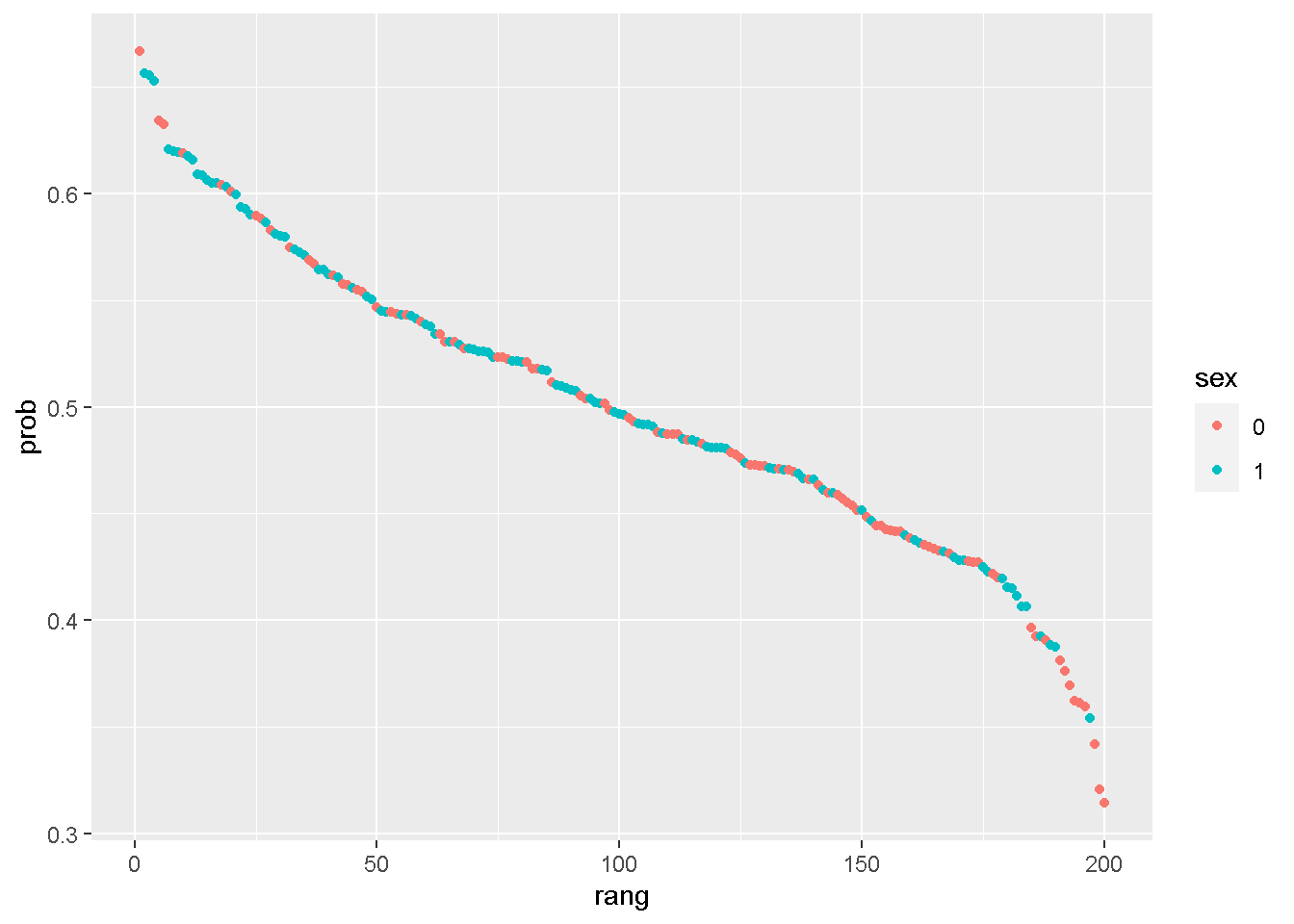
Atteslander, Peter. 2003. Methoden der empirischen Sozialforschung. Berlin: De Gruyter.
Langenscheidt. 2017. “Langenscheidt Fremdwörterbuch Online.”
Manderscheid, Katharina. 2012. Sozialwissenschaftliche Datenanalyse mit R: Eine Einführung. 1st ed. Wiesbaden: VS Verlag für Sozialwissenschaften.