Kapitel 13 t-Test (und U-Test)
13.1 Problemstellung
Wir möchten herausfinden, ob es einen Unterschied bei der Einschätzung der Lernkultur basierend auf dem Geschlecht der StudienteilnehmerInnen gibt.
13.2 Anknüpfungspunkte
- Unterschiedshypothese
- Hypothesentest
13.3 Allgemeines
- Ziel: Vergleich von zwei Stichprobenmittelwerten
- Arten
- unabhängige Stichproben: Keine Beobachtung bzw. Messung wird von einer anderen beeinflusst. Beispiel: eine Gruppe StudentInnen wird zufällig in zwei gleichgroße Gruppen geteilt. Gruppe 1 nimmt an einem Lerntutorium teil, Gruppe 2 nicht. Die zwei Gruppen sind unabhängig voneinander.
- abhängige Stichproben: die Messungen werden voneinander beeinflusst. Beispiel: eine Gruppe von StudentInnen nimmt an einem Lerntutorium teil. Ein Forscher vergleicht sodann die Lernkompetenz der StudentInnen vor und nach dem Lerntutorium.
- Hypothesentest
- H0: es existiert kein Unterschied zwischen zwei Gruppen.
- H1: es existiert ein Unterschied zwischen zwei Gruppen.
- Logik des t-Tests
- Gruppenmittelwerte berechnen
- Differenz der Gruppenmittelwerte berechnen
- Signifikanz der Differenz berechnen
13.4 Voraussetzungen t-Test
- Randomisierung = Zufallsstichprobe
- mindestens intervallskalierte Daten. Bei ordinalskalierten Daten kannst du auf den Mann-Whitney-U-Test (unabhängige Stichproben) bzw. den Wilcoxon-Vorzeichen-Rang-Test (gepaarte Stichproben) ausweichen.
- Normalverteilung der Variablen. Test: Kolmogorov-Smirnov-Test (sollte nicht signifikant sein!). Bei nicht normalverteilten Daten kannst du auf den Mann-Whitney-U-Test (unabhängige Stichproben) bzw. den Wilcoxon-Vorzeichen-Rang-Test (gepaarte Stichproben) ausweichen.
- Varianzhomogenität: gleiche Varianzen der Gruppen. Test: Levene-Test (Ergibt sich hier ein signifikanter F-Wert, dann darf nicht von Varianzhomogenität ausgegangen werden)
13.5 Beispiel
Datei: ttest1.csv (Simulierte Daten)
- Variablen
- Wert
- Gruppe (0, 1, 2)
- 0 bzw. 1 = zufällig Daten (“männlich / weiblich”)
- 2 = manipulierte Daten
13.6 Umsetzung mit Software
In SPSS:
In PSPP:
13.6.1 Beispiel - Visualisierung
Diese drei Boxplots zeigen die Verteilungen von “Wert” in den drei Gruppen (0, 1, 2).
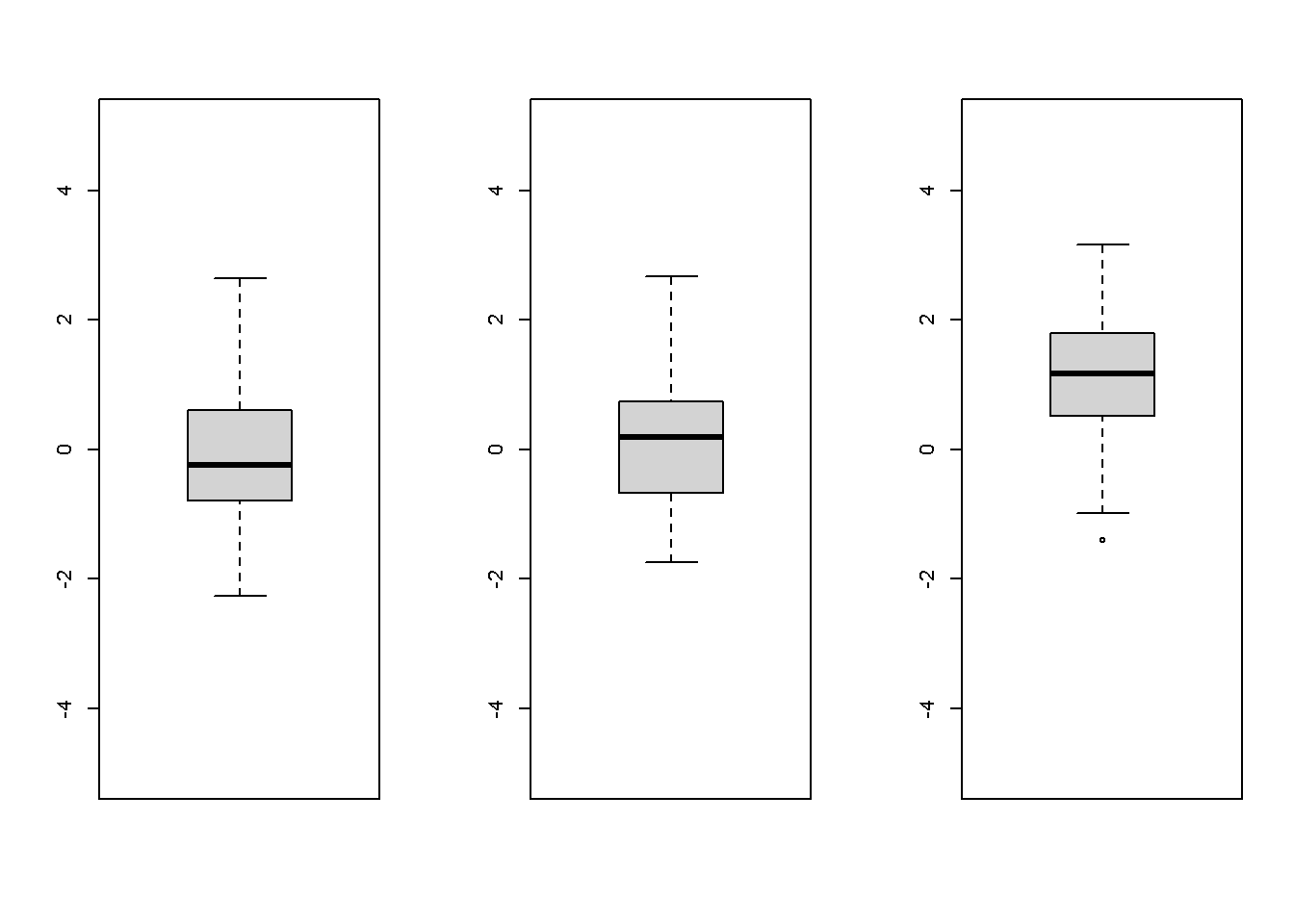
13.6.2 Beispiel - t-Test Gruppen 0/1
Wir führen einen t-Test zwischen den Gruppen 0 und 1 durch.
##
## Welch Two Sample t-test
##
## data: df$Wert[df$Gruppe == 0] and df$Wert[df$Gruppe == 1]
## t = -0.6, df = 144, p-value = 0.5
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.43 0.22
## sample estimates:
## mean of x mean of y
## -0.076 0.02813.6.3 Beispiel - t-Test Gruppen 0/1: Interpretation
Beachte bei der Interpretation…
- den Konfidenzintervall von -0.43 bis 0.22
- den p-Wert von 0.53
Frage: Was sagen diese Werte aus?
13.6.4 Beispiel - t-Test Gruppen 0/2
Wir führen einen t-Test zwischen den Gruppen 0 und 2 durch.
##
## Welch Two Sample t-test
##
## data: df$Wert[df$Gruppe == 0] and df$Wert[df$Gruppe == 2]
## t = -7, df = 115, p-value = 7e-10
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.55 -0.84
## sample estimates:
## mean of x mean of y
## -0.076 1.11813.6.5 Beispiel - t-Test Gruppen 0/2: Interpretation
Beachte bei der Interpretation…
- den Konfidenzintervall von -1.55 bis -0.84
- den p-Wert von 0
Achtung: Der p-Wert ist natürlich nicht genau 0 (siehe Output des Tests)–aber durch Rundungen könnte es so aussehen. Bei eigenen Texten bzw. der Interpretation daher < 0.001 verwenden.
und, da es sich um ein statistisch signifikantes Ergebnis handelt
- die Mittelwerte der Gruppen von -0.08 bzw. 1.12.
Frage: Was sagen diese Werte aus?
13.7 Übung
Lade die Daten Froehlich 2014 Daten 100.sav
Führe den Kolmogorov-Smirnov (K-S) Test für die Variablen WC1 bis WC7 durch. Was wird hier getestet?
Was bedeuten signifikante Ergebnisse im K-S Test?
Wie lautet H0 des K-S Test?
Wie viele der getesteten Variablen WC1 bis WC7 sind laut K-S Test wahrscheinlich normalverteilt?
Führe den Kolmogorov-Smirnov (K-S) Test für eine neu generierte Index-Variable MWC durch, die durch den Mittelwert von WC1 bis WC7 gebildet wird. Liegt eine Normalverteilung laut K-S Test vor?
Angenommen die Index-Variable MWC ist normalverteilt: Wie kannst du dieses unterschiedliche Ergebnis im Vergleich zu WC1-WC7 erklären?
Wir wollen die MWC-Werte zweier Banken vergleichen. Welchen Test wählst du?
Teste den Unterschied zwischen Bank 2 und Bank 4. Liegt ein signifikanter Unterschied vor? Welche Bank hat den höheren Wert im Durchschnitt?
Teste den Unterschied zwischen Bank 3 und Bank 4. Liegt ein signifikanter Unterschied vor? Welche Bank hat den höheren Wert im Durchschnitt?
Versuche den Mann-Whitney-U-Test zwischen Bank 3 und Bank 4 durchzuführen. Welches Problem ergibt sich?
Erstelle die Variable bank34, die den Wert 3 für alle Antworten aus DBAN = 3 und den Wert 4 für alle Antworten aus DBAN = 4 enthält (und ansonsten nur Leerzellen). Führe mit dieser Variable den Mann-Whitney-U-Test zwischen Bank 3 und Bank 4 basierend auf MWC durch.
13.8 Lösung
Es wird die Normalverteilung der Variablen getestet.
Es liegt laut K-S Test keine Normalverteilung vor.
Die Daten liegen in einer bestimmten Distribution (Normalverteilung) vor.
0
Ja
Indexvariablen sind durch die verschiedenen Messungen die zusammengefasst werden (WC1-WC7) eher normalverteilt als ihre Komponenten. Das haben wir in Einheit 1 und 2 diskutiert.
T-Test bei unabhängigen Stichproben.
Das Ergebnis ist nicht signifikant (p = .526); Bank 2 hat den höheren Mittelwert (2,9341).
Das Ergebnis ist signifikant (p = .012); Bank 3 hat den höheren Mittelwert (3,6250).
SPSS verlangt nach einer Variable mit nur 2 Dimensionen.
13.9 Student Voice
Der T-Test dient dem Vergleich zweier unabhängiger Stichproben bezüglich eines metrischen Merkmals. Die Vorrausetzung für den Test ist, dass die Daten mindestens intervallskaliert sind. Außerdem ist eine Normalverteilung der Daten wichtig. Sollten die Daten nicht intervallskaliert und normalverteilt sein, wendet man bei unabhängigen Stichproben den Mann-Whitney-U - Test an und bei gepaarten Stichproben den Wilcoxon-Vorzeichen-Rang- Test. Der T-Test setzt außerdem eine Varianzhomogenität voraus. Die Varianzen der beiden Gruppen sollen also gleich groß sein.
Zunächst einmal testet der T - Test, ob die Mittelwerte der Grundgesamtheit verschieden sind. Anschließend wird die Differenz der Mittelwerte berechnet und ihre gemeinsame Varianz. Liegt die Varianz dann über 0,05 spricht man von einer Varianzgleichheit und lehnt die Nullhypothese nicht ab. Sprich, man geht schon einmal von einer Varianzgleichheit aus.
Nach der Berechnung der gemeinsamen Varianz wird der t - Wert berechnet. Da dieser in PSPP angezeigt nicht großartig interpretierbar ist, schaut man sich für die Interpretation den p - Wert an. Jeder t - Wert hat nämlich einen p - Wert, welchen man sich ohne PSPP anhand des T - Wertes nachschlagen müsste.
Liegt der p - Wert über 0,05 wird davon ausgegangen, dass man die Nullhypothese annehmen kann. Man spricht dann also von keinem signifikanten Unterschied unter den getesteten Gruppen/ Stichproben.
13.10 Übung
Führe einen t-test zwischen den Gruppen 0 und 1 bei den Datensätzen ttest2.csv und ttest3.csv durch.
13.11 Lösung ttest2.csv
13.11.1 Levene Test
## Warning: package 'car' was built under R version 4.0.3## Loading required package: carData## Warning: package 'carData' was built under R version 4.0.3## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.62 0.44
## 1813.11.2 t-test
## [1] "Varianzhomogenität angenommen"##
## Two Sample t-test
##
## data: df2$Wert[df2$Gruppe == 0] and df2$Wert[df2$Gruppe == 1]
## t = 0.8, df = 18, p-value = 0.5
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.49 1.03
## sample estimates:
## mean of x mean of y
## 0.076 -0.198## [1] "Varianzhomogenität nicht angenommen (nach Welch)"##
## Welch Two Sample t-test
##
## data: df2$Wert[df2$Gruppe == 0] and df2$Wert[df2$Gruppe == 1]
## t = 0.8, df = 18, p-value = 0.5
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.49 1.03
## sample estimates:
## mean of x mean of y
## 0.076 -0.198Beachte bei der Interpretation…
- den Konfidenzintervall von -0.49 bis 1.03
- den p-Wert von 0.46
- die Mittelwerte der Gruppen von 0.08 bzw. -0.2
- die Voraussetzungen für den t-Test
13.12 Lösung ttest3.csv
13.12.1 Levene Test
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.27 0.61
## 199813.12.2 t-test
## [1] "Varianzhomogenität angenommen"##
## Two Sample t-test
##
## data: df3$Wert[df3$Gruppe == 0] and df3$Wert[df3$Gruppe == 1]
## t = -2, df = 1998, p-value = 0.02
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.193 -0.014
## sample estimates:
## mean of x mean of y
## 0.037 0.140## [1] "Varianzhomogenität nicht angenommen (nach Welch)"##
## Welch Two Sample t-test
##
## data: df3$Wert[df3$Gruppe == 0] and df3$Wert[df3$Gruppe == 1]
## t = -2, df = 1998, p-value = 0.02
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.193 -0.014
## sample estimates:
## mean of x mean of y
## 0.037 0.140Beachte bei der Interpretation…
- den Konfidenzintervall von -0.19 bis -0.01
- den p-Wert von 0.02
- die Mittelwerte der Gruppen von 0.04 bzw. 0.14
- die Voraussetzungen für den t-Test