Kapitel 8 Lage und Streuung

8.1 Anknüpfungspunkte

Variablen
Skalenniveaus

8.2 Beispieldaten

Hier sind die Beispieldaten, die für die Kapitel Lagemaße und Streumaße für händische Berechnungen verwendet werden.

## [1]  1 20  5  5  5  7  9 10 12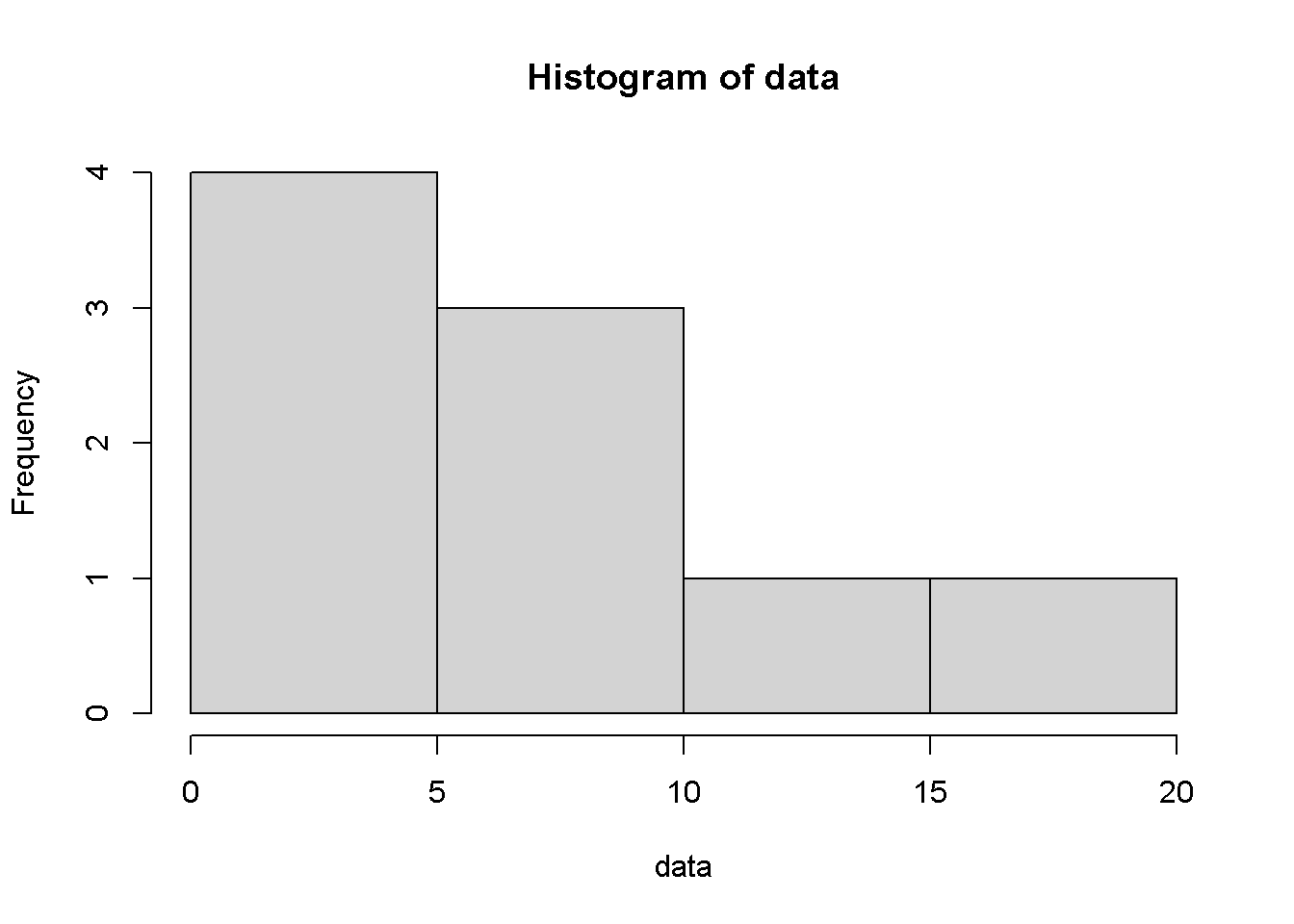

8.3 Lagemaße (Maße der zentralen Tendenz)

8.3.1 Modus (Modalwert)

Der Modus ist jener Wert, der in einer diskreten Verteilung am häufigsten vorkommt.

Vorteil: Ausreißer-resistent.
In einer grafischen Darstellung zeigt sich der Modalwert als Maximum. Die Berechnung des Modalwerts erfordert Nominalskalenqualität der Variablen. Graphen mit einem Modus und ohne weitere relative Hochpunkte heißen unimodal, eingipfelig; Gibt es in einer Verteilung zwei voneinander getrennte gleich hohe Maximalwerte -> bimodale Verteilung

Frage: Berechne den Modus der Beispieldaten.

table(data)

## data
##  1  5  7  9 10 12 20 
##  1  3  1  1  1  1  1

as.numeric(names(sort(-table(data)))[1])

## [1] 5

8.3.2 Median

Der Median ist jener Wert der eine Verteilung in zwei Hälften teilt. Der Median teilt eine Verteilung in zwei Hälften (es liegen genauso viele Messwerte über sowie unter diesem Wert) Der Median setzt mindestens ordinalskalierte Daten voraus Vorteil: Ausreißer-unempfindlich! Händische Berechnung: Daten sortieren, dann die Mitte suchen (bei gerader Anzahl an Werten: arithmetisches Mittel der beiden mittleren Zahlen.

Frage: Berechne den Median der Beispieldaten.

sort(data)

## [1]  1  5  5  5  7  9 10 12 20

median(data)

## [1] 7

8.3.3 Arithmetisches Mittel (\(\mu\), \(\bar{x}\), Mittelwert)

Das arithmetische Mittel gibt den Durchschnitt aller Messergebnisse wieder. Das gebräuchlichste Maß der zentralen Tendenz. Gibt den Durchschnitt aller Messergebnisse wieder. Ist die Summe aller Werte dividiert durch deren Anzahl n. Die Berechnung des arithmetischen Mittels ist nur bei mind. intervallskalierten Daten möglich. Achtung: empfindlich gegenüber Ausreißern.

\[ \bar{x} = \frac{1}{n}*\sum_{i=1}^{n}(x) \]

Frage: Berechne das arithmetische Mittel der Beispieldaten.

mean(data)

## [1] 8.2

8.4 Schiefe und Kurtosis

8.4.1 Schiefe (skew, v)

Beschreibt die Asymmetrie einer Verteilung.

Der Datensatz “lm_rechts.csv” ist rechtsschief.

median(rechts)

## [1] 0.26

mean(rechts)

## [1] 0.28

Der Datensatz “lm_links.csv” ist linksschief.

median(links)

## [1] 0.74

mean(links)

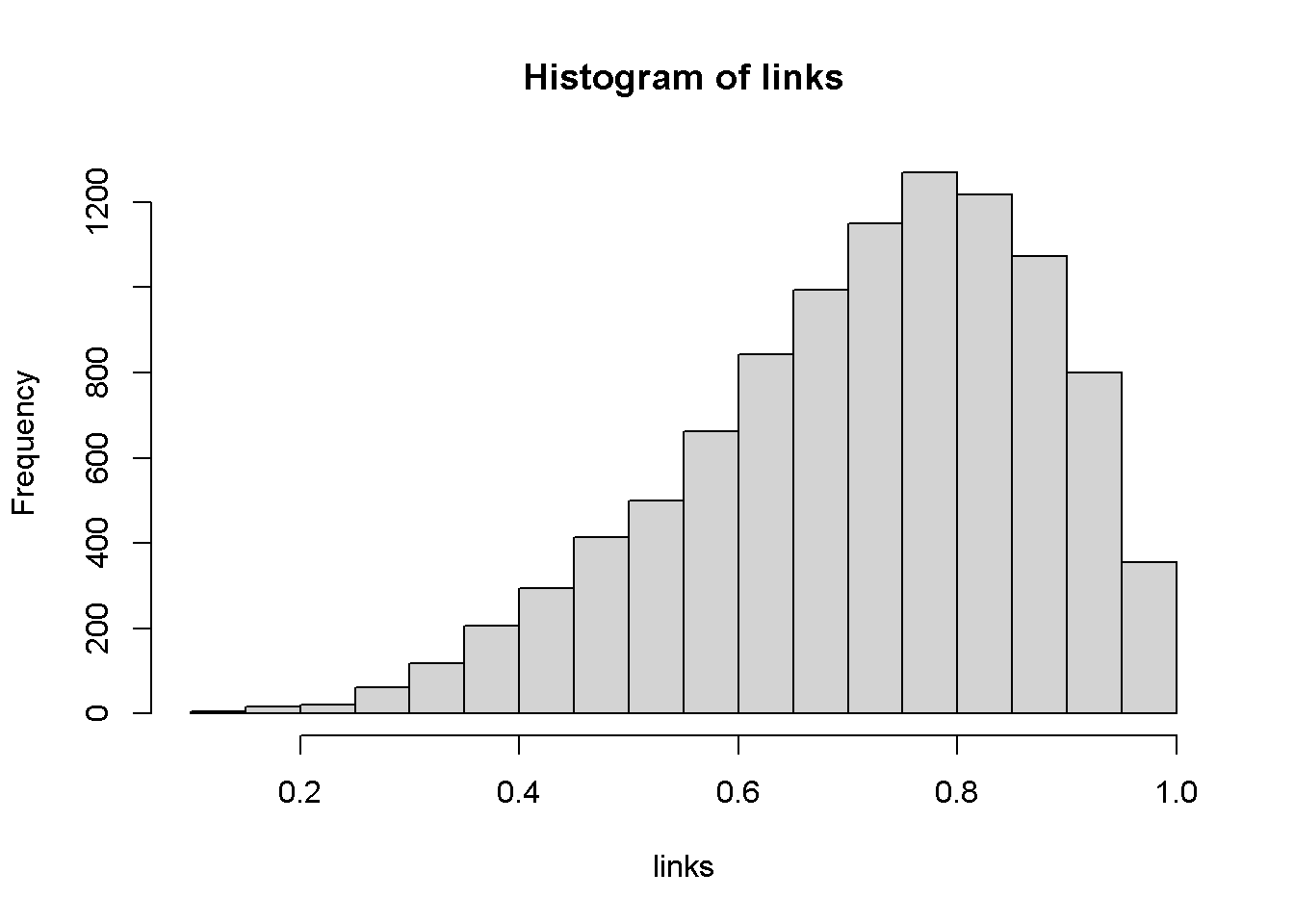
## [1] 0.72

Frage: Wie kann man dieses Histogramm in SPSS darstellen?

Antwort TBA

8.4.2 Kurtosis (Wölbung)

Kurtosis beschreibt die Steilheit einer Verteilung.

Der Datensatz “lm_steil.csv” ist steilgipfelig.

Der Datensatz “lm_flach.csv” ist flachgipfelig.

8.5 Quantile, Quartile, Dezile, Perzentile

Quantil: der Wert, der eine Verteilung in bestimmte Segmente aufteilt.
- Quartile: teilen einen geordneten Datensatz in vier gleiche Teile
- Dezile: teilen einen geordneten Datensatz in 10 gleiche Teile
- Perzentile: teilen einen geordneten Datensatz in 100 gleich große Teile

Quartile bei den Beispieldaten:

##   0%  25%  50%  75% 100% 
##    1    5    7   10   20

Das 34. Quantil (=34% Perzentil, Zahl willkürlich gewählt) bei den Beispieldaten:

## 34% 
##   5

Achtung: Es gibt keine einheitliche Berechnungsweise für die Quartile!

8.6 Streuungsmaße

Streuungsmaße beschreiben, wie stark die einzelnen Werte in einer Verteilung vom Mittelwert abweichen

8.6.1 Spannweite (Range)

Die Spannweite gibt die Größe des Bereichs an, in dem die Messwerte liegen. Sie berechnet sich über die Differenz aus dem größten und dem kleinsten Wert. Die Variationsbreite sagt zwar einiges über die Verteilung aus, aber wie genau die Messwerte variieren, ist aus ihr alleine nicht ersichtlich.

\[ range = max(x) - min(x) \]

Frage: Berechne die Spannweite der Beispieldaten.

max(data)-min(data)

## [1] 19

8.6.2 (Inter-)Quartilsabstand (IQR)

Der Quartilabstand IQR ist definiert als die Differenz zwischen dem 1. Quartil und dem 3. Quartil. Damit enthält er die zentralen 50% einer Verteilung. Aussagen über Streuung können getroffen werden; im Vergleich zur Spannweite gegenüber Ausreißern stabiler.

\[ IQR = Q_{0.75}(x)-Q_{0.25}(x) \]

Frage: Berechne den IQR der Beispieldaten.

print(quantile(data))

##   0%  25%  50%  75% 100% 
##    1    5    7   10   20

x <- quantile(data)[4] - quantile(data)[2] 
print(unname(x))

## [1] 5

8.6.3 Varianz (\(\sigma^2\), \(s^2\), Var)

Kann für mindestens intervallskalierte Daten berechnet werden
Berechnet sich aus der Summe der quadrierten Abweichungen aller Messwerte vom arithmetischen Mittel, dividiert durch die Anzahl aller Messwerte
Die Varianz nimmt als umso größere Werte an, je stärker die Messwerte von ihrem Mittelwert abweichen.

\[ Var(x) = s^2 = \frac{1}{n-1}*\sum_{i=1}^{n}\left( x_i - \bar{x} \right)^2\]

Hinweis: Vielleicht findest du wo anders auch eine Formel, in der nur durch n statt nur (n-1) dividiert wird. Das ist die Formel für die Varianz der Population. Für die Varianz der Stichprobe ist n-1 präziser.

Schauen wir uns nochmal die Formel (der Population) genau an um zu verstehen, was sie bedeutet. Betrachten wir die Teile im Einzelnen.

\[ \frac{1}{n}*\sum_{i=1}^{n}\left( \dots \right)^2\]

Das sollte uns an den Mittelwert erinnern. Was wir also berechnen, ist ein Durchnschnitt von etwas. Aber von was?

\[ \left( x_i - \bar{x} \right)^2\]

Dieser Teil zeigt uns, dass es um (quadrierte) Abstände geht (die Abstände zwischen den jeweiligen Werten des Datensatzes und dem Mittelwert des Datensatzes). Warum wird quadriert? Das wird gemacht, damit sich positive und negative Abstände nicht (zu Null) summieren. Uns interessieren die absoluten Abstände (und eine quadrierte Zahl ist auf jeden Fall positiv)

Frage: Berechne die Varianz der Beispieldaten.

var(data)

## [1] 30

Frage: Berechne die Varianz der Daten {1, 2, 6} händisch.

dat <- c(1, 2, 6)
(n <- length(dat))

## [1] 3

(x <- mean(dat))

## [1] 3

(zaehler <- (1-x)^2+(2-x)^2+(6-x)^2)

## [1] 14

(var_pop <- zaehler/n)

## [1] 4.7

(var_sample <- zaehler/(n-1))

## [1] 7

8.6.4 Standardabweichung (\(\sigma\), \(s\), SD)

Die Standardabweichung ist definiert als die Wurzel der Varianz. Varianz und Standardabweichung sind relative Maßzahlen; sie können immer nur in Relation zum arithmetischen Mittel und/oder anderen Varianzen und Standardabweichungen sinnvoll interpretiert werden.

Wie sehr streut die Verteilung (A) gegenüber der Verteilung (B)?

Besonderheit Normalverteilung:

68,3% der Beobachtungen im Intervall +/- s
95,4% der Beobachtungen im Intervall +/- 2s
99,7% der Beobachtungen im Intervall +/- 3s

\[ s = \sqrt{Var(x)}\]

Frage: Berechne die Standardabweichung der Beispieldaten.

sd(data)

## [1] 5.5

8.6.5 Exkurs: Statistik vs. Parameter

Sind alle Merkmalsausprägungen der Grundgesamtheit bekannt, wird die Standardabweichung der Grundgesamtheit verwendet, zum Beispiel wenn ein Lehrer berechnen will, wie gut seine SchülerInnen durchschnittlich bei einem Test abgeschnitten haben und wie die Ergebnisse verteilt sind.

Im Bereich der Bildungswissenschaften wird man selten alle Werte kenne. Durch eine Studie (Umfrage, …) kennt man die Merkmalsausprägungen der Personen der Stichprobe. Berechnet man hier die Standardabweichung, wird jene der Stichprobe verwendet. ### Variationskoeffizient

\(cv = \frac{s}{\bar{x}}\)

8.7 Übungen “per Hand”

Berechne alle besprochenen Lage- und Streuungsmaße der folgenden Daten mit der Hand / dem Taschenrechner.

8.7.1 Datensatz 1

## [1] 9 4 7 1 2

8.7.2 Datensatz 2

## [1] 5 6 6 8 1 1

8.7.3 Datensatz 3

## [1]  5 10  7  4 10

8.7.4 Lösung zu Datensatz 1

##   modus median mittelwert iqr  sd var
## 1     1      4        4.6   5 3.4  11

8.7.5 Lösung zu Datensatz 2

##   modus1 modus2 median mittelwert iqr  sd var
## 1      1      6    5.5        4.5   4 2.9 8.3

8.7.6 Lösung zu Datensatz 3

##   modus median mittelwert iqr  sd var
## 1    10      7        7.2   5 2.8 7.7

8.8 Übungen mit Software

Berechne alle besprochenen Lage- und Streuungsmaße der Daten aus Datei “Daten 1.csv” mit dem Computer

8.8.1 Lösung

##   modus median mittelwert iqr  sd   var
## 1   379    482        504 495 288 83048

8.9 Umsetzung in Software

In PSPP