Kapitel 14 Varianzanalyse (ANOVA)
14.1 Problemstellung
Wir wollen feststellen, ob es hinsichtlich des Lernklimas Unterschiede zwischen den fünf teilnehmenden Organisationen gibt.
Frage: Wieso ist hier ein t-Test nicht zielführend?
14.2 Anknüpfungspunkte
- Hypothesentest
- t-Test
14.3 Allgemeines
- Mehrere Gruppenmittelwerte werden verglichen
- H0: In der Grundgesamtheit sind alle Mittelwerte gleich
- H1: In der Grundgesamtheit sind nicht alle Mittelwerte gleich
- Grundprinzip
- Varianzen innerhalb der Gruppen berechnen: Streuung der Werte innerhalb der Gruppen um den jeweiligen Stichprobenmittelwert (SSR); beschreibt die Unterschiede zwischen den Merkmalsausprägungen innerhalb einer Stichprobe.
- Varianzen zwischen den Gruppen berechnen: Streuung der Gruppemittelwerte um den Gesamtmittelwert (SSM); spiegelt die Unterschiede wider, die aufgrund der Zugehörigkeit zu den verschiedenen Gruppen (z.B. durch verschiedenen Unterrichtsformen in den Schulklassen) entstanden sind.
- Vergleich dieser Varianzen (F-Test): Je höher der F-Wert (je größer SSM im Verhältnis zu SSR), desto eher gibt es einen Unterschied.
14.4 Post-Hoc Tests
- F-Wert gibt nur an, ob es einen Unterschied gibt oder nicht
- Man weiß nicht, wo (zwischen welchen Gruppen) es einen Unterschied gibt
- Logik von Post-Hoc Tests
- t-Tests: zwischen allen Gruppen werden t-Tests durchgeführt
- Korrektur um \(\alpha\)-Inflation: bei mehrfachem Testen in derselben Grundgesamtheit steigt die Wahrscheinlichkeit einen Fehler 1. Art zu begehen mit der Anzahl der Testdurchführungen
14.5 Voraussetzungen ANOVA
- Intervallskalierte Daten
- Normalverteilung der abhängigen Variablen: Wenn nicht gegeben auf Kruskal Wallis Test ausweichen
- Homogenität der Varianzen: Wenn nicht gegeben auf Brown-Forsythe’s F oder Welch’s F ausweichen
14.6 Beispiel - ANOVA (ttest1.csv)
Gibt es Unterschiede?
## Df Sum Sq Mean Sq F value Pr(>F)
## Gruppe 2 51.7 25.85 26.7 5.6e-11 ***
## Residuals 197 190.9 0.97
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1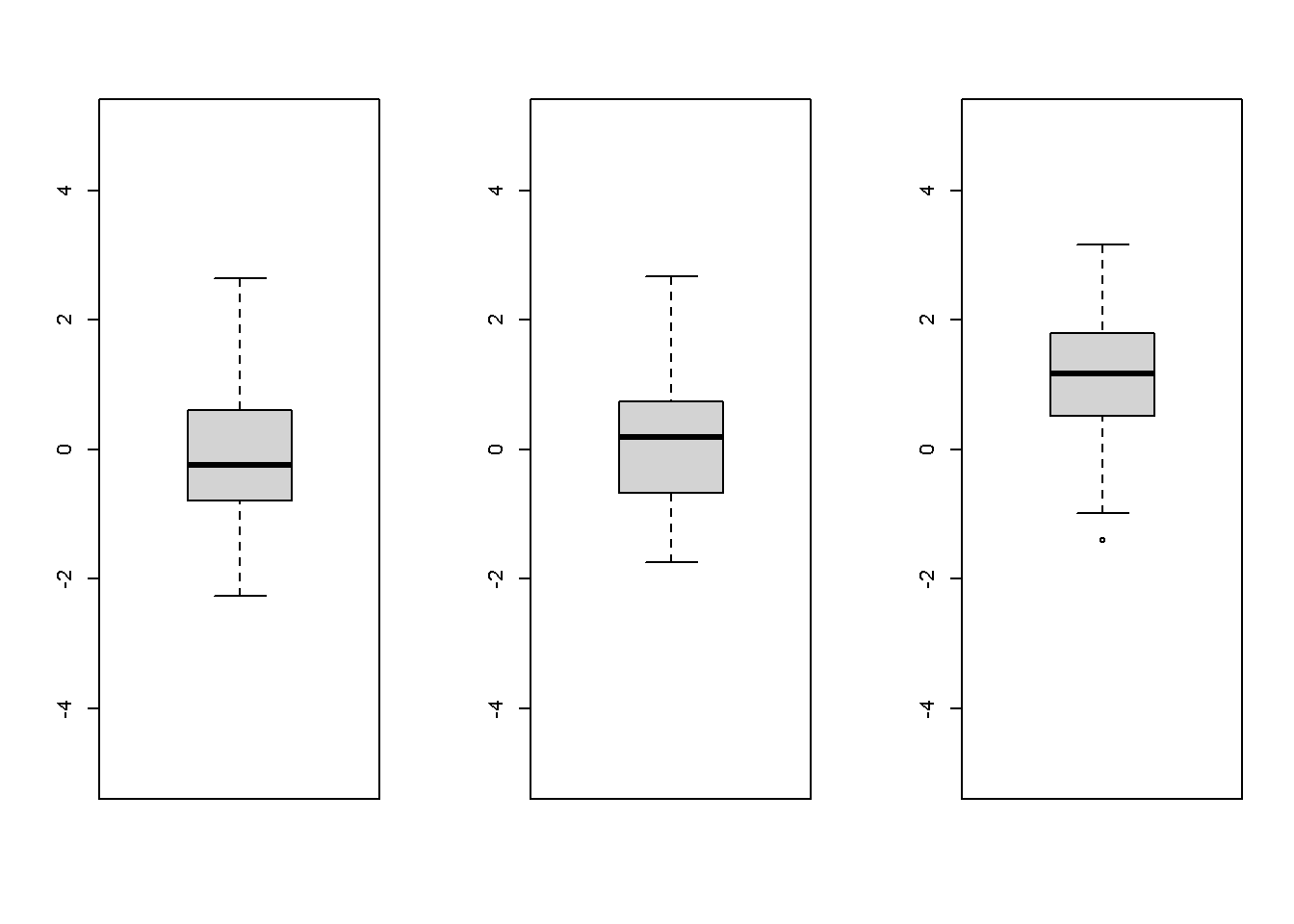
Wo gibt es Unterschiede?
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = Wert ~ Gruppe, data = df)
##
## $Gruppe
## diff lwr upr p adj
## 1-0 0.1 -0.28 0.49 0.8
## 2-0 1.2 0.77 1.61 0.0
## 2-1 1.1 0.67 1.51 0.014.7 Exkurs: ANOVA mit der Hand
## [1] "Accept H0"14.8 Student Voice
Ähnlich wie beim t-Test bei unabhängigen Stichproben lässt sich mit der ANOVA eine Hypothese überprüfen, derzufolge eine Variable in unterschiedlichen Teilgruppen der Grundgesamtheit einen gleich hohen Mittelwert aufweist. Ein wesentlicher Unterschied zum t-Test ist zunächst einmal, dass sich mit der ANOVA mehrere Mittelwerte (mehrere Teilgruppen der Grundgesamtheit) miteinander vergleichen lassen, während der t-Test nur den Vergleich zweier Mittelwerte ermöglicht. Die mit der ANOVA getestete Nullhypothese unterstellt, alle miteinander verglichenen Gruppenmittelwerte der betrachteten Variablen seien in der Grundgesamtheit identisch. Außerdem werden auch multiple Vergleichtests durchgeführt, mit denen identifiziert werden kann, zwischen welchen beobachteten Gruppen signifikante Mittelwertunterschiede bestehen.
Wenn das Ergebnis signifikant (p< 0,05) ist, bedeutet dies, dass es Unterschiede gibt. Die Frage ist nur: zwischen welchen Gruppen?
Ein Post-hoc-Test (z.B. Scheffe-Test in SPSS) gibt Auskunft darüber, wo genau Differenzen zu finden sind.
14.9 Übung
Führe eine Varianzanalyse basierend auf dem Datensatz “anova1.csv” aus. “grp” ist der Faktor, “y” die abhängige Variable. Teste auch alle Voraussetzungen.
14.9.1 Lösung
## Df Sum Sq Mean Sq F value Pr(>F)
## grp 4 205 51.4 178 <2e-16 ***
## Residuals 685 197 0.3
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1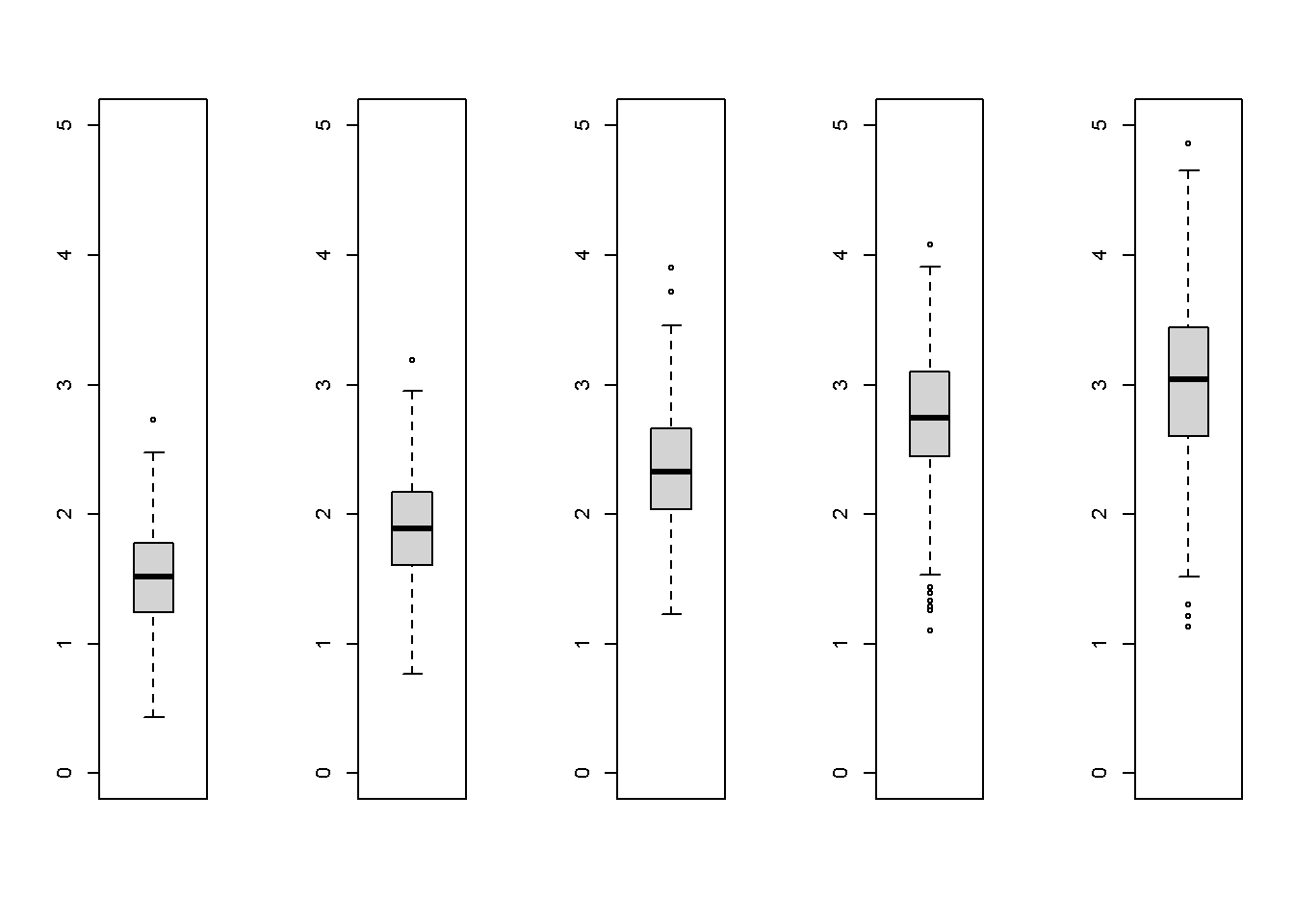
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = y ~ grp, data = df)
##
## $grp
## diff lwr upr p adj
## 1-0 0.36 0.18 0.54 0
## 2-0 0.84 0.67 1.01 0
## 3-0 1.18 1.01 1.36 0
## 4-0 1.50 1.33 1.67 0
## 2-1 0.48 0.30 0.66 0
## 3-1 0.82 0.64 1.00 0
## 4-1 1.14 0.96 1.32 0
## 3-2 0.34 0.17 0.52 0
## 4-2 0.66 0.49 0.83 0
## 4-3 0.32 0.14 0.50 0